Singularity theory explains topological defects in LC droplets

 22 Decemnber 2019

In a joint publication in Physical Review X, researchers of the University of Warwick, UK, University of Ljubljana, Slovenija and J. Stefan Institute, Slovenija, explain why topological defects of higher charges are arranged in intriguing patterns inside a droplet of a chiral nematic liquid crystal. Read more.

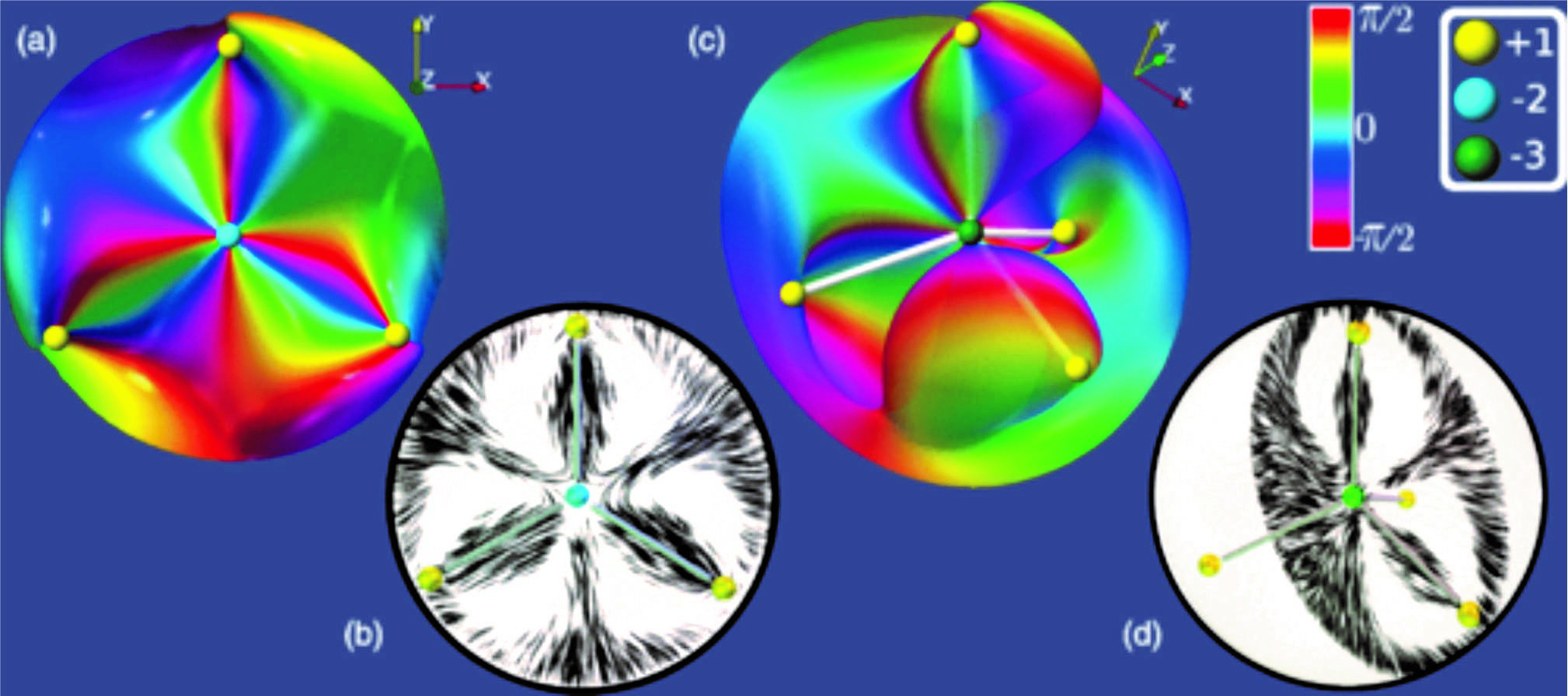
Chiral nematic liquid crystal is made of chiral molecules and exhibits a spontaneously twisted structure in the ground state. The direction of spontaneous twist is perpendicular to the local direction of molecules (called a director) and is named the helical pitch. When such a liquid forms spherical droplet, there is a frustration for the liquid crystal as of how to align in such a spherical confinement. For decades this problem has been intriguing researchers, who were able to see defects inside the droplets, but were unable to tell what kind of defects are. In a series of experiments, Gregor Posnjak of JSI has used Fluorescent Confocal Polarized Microscope to decipher the ordering of the liquid crystal inside the droplets. He has found that defects in chiral nematic droplets are organized in a regularly fashion, mimicking the spatial distribution of atoms in molecules: defects are like atoms, which are connected to each other by the elastic liquid crystal. Moreover, Posnjak for the first time discovered higher topological charges. Like electric charges, topological charges are special points in director field, where the degree of orientational order is zero. Now, elementary electric charges carry a unit charge only, but topological charges can carry a multiple of “quanta” of topological charge. While the identification of higher charges could be carried out by careful analysis of experimental images, the explanation and mathematical background remained unexplained.

Now, in an article published in Physical Review X, Joseph Pollard, Gregor Posnjak, Simon Čopar, Igor Muševič, and Gareth P. Alexander, provide a characterization of point defects in droplets of cholesteric liquid crystal, using a combination of experiment, simulation, and theoretical analysis. They show that there are certain defects that are incompatible with a uniform sense of chiral twisting for topological reasons. Furthermore, those defects that are compatible with twist of a single handedness are shown to have the structure of the gradient field of an isolated critical point and, hence, are described by singularity theory. They show that the mathematical tools of singularity theory reproduce, with excellent agreement, the experimental observations of high charge defects and topological molecules. The results have implications beyond liquid crystal droplets in characterizing chiral materials and their topology in general.